Логарифмом числа 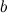 по основанию
по основанию  (
( 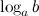 ) называется такое число
) называется такое число  , что
, что 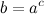 , то есть записи
, то есть записи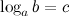 и
и 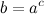 равносильны. Логарифм имеет смысл, если
равносильны. Логарифм имеет смысл, если 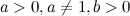 .
.
Меню сайта
Преобразование графика функции
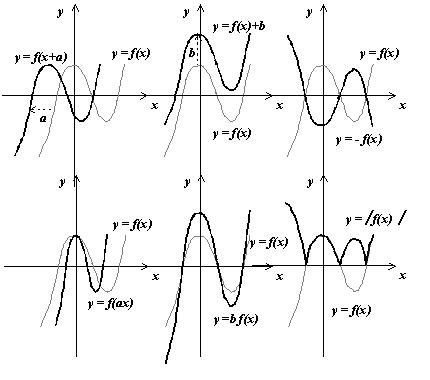
Преобразования графиков функций — это линейные преобразования функции y = f(x) или её аргумента x к виду y =af(kx + b) + m, а также преобразование с использованием модуля.
Зная, как строить графики функции y = f(x), где y = kx + b, y = ax2, y = xn , y=xk, y = sin x, y = cosx, y = tgx, y = ctgx, y=ax![]() y=logax, можно построить график функции y = af(kx + b) + m.
y=logax, можно построить график функции y = af(kx + b) + m.
|
Общий вид функции |
Преобразования |
|
y = f(x - b) |
Параллельный перенос графика вдоль оси абсцисс на | b | единиц
|
|
y = f(x + b) |
|
|
y = f(x) + m |
Параллельный перенос графика вдоль оси ординат на | m | единиц
|
|
Отражение графика |
|
|
y = f( - x) |
Симметричное отражение графика относительно оси ординат. |
|
y = - f(x) |
Симметричное отражение графика относительно оси абсцисс. |
|
Сжатие и растяжение графика |
|
|
y = f(kx) |
|
|
y = kf(x) |
|
|
Преобразования графика с модулем |
|
|
y = | f(x) | |
|
|
y = f( | x | ) |
|
Если немного перефразировать - Логарифм числа 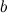 по основанию
по основанию  определяется как показатель степени, в которую надо возвести число
определяется как показатель степени, в которую надо возвести число  , чтобы получить число
, чтобы получить число 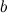 (Логарифм существует только у положительных чисел).
(Логарифм существует только у положительных чисел).
Логарифм в переводе с греческого буквально означает "число, изменяющее отношение".

|
|
|||
Метод рационализации
